Evolutionary Computation

Multi-objective Optimization


Multi-objective Optimization


The study of optimizing more than one objective function simultaneously.


  • Multi-objective evolutionary algorithms
  • Pareto dominance
  • NSGA-II
  • Many-objective optimization
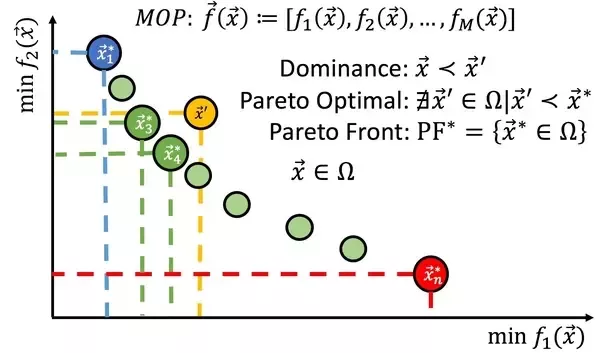
    • If F(x) = f_1(x), f_2(x), ...

MOEAs


Multi-objective evolutionary algorithms

  • NSGA: Srinivas, Nidamarthi, and Kalyanmoy Deb. "Muiltiobjective optimization using nondominated sorting in genetic algorithms." Evolutionary computation 2.3 (1994): 221-248.
  • SPEA2: Zitzler, Eckart, Marco Laumanns, and Lothar Thiele. "SPEA2: Improving the strength Pareto evolutionary algorithm." TIK-report 103 (2001).
  • NSGA-II: Deb, Kalyanmoy, et al. "A fast and elitist multiobjective genetic algorithm: NSGA-II." IEEE transactions on evolutionary computation 6.2 (2002): 182-197.
  • Deb, Kalyanmoy (2001) Multi-objective optimization using evolutionary algorithms. John-Wiley, Chichester
  • MOEA/D: Zhang, Qingfu, and Hui Li. "MOEA/D: A multiobjective evolutionary algorithm based on decomposition." IEEE Transactions on evolutionary computation 11.6 (2007): 712-731.
  • SMS-EMOA: Beume, N., Naujoks, B., & Emmerich, M. (2007). SMS-EMOA: Multiobjective selection based on dominated hypervolume. European Journal of Operational Research, 181(3), 1653-1669.
  • Emmerich, Michael TM, and AndrĂ© H. Deutz. "A tutorial on multiobjective optimization: fundamentals and evolutionary methods." Natural computing 17.3 (2018): 585-609. [pdf]

Travelling Salesman Problem


Pareto dominance


    A solution is said to Pareto dominate another if it is more optimal in all dimensions.
    Solutions which are not dominated by any other are called "non-dominated".

Why dominance?



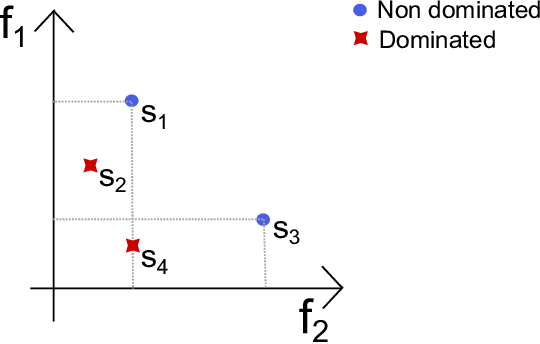
    In single-objective problems it's easy to find the highest performing individual - highest fitness.
    In multi-objective problems the the highest performing individual in an objective could be horrible in another objective!
  • We have f_1(S1) < f_1(S3) and f_2(S1) > f_2(S3) -> S1 and S3 are equally good.

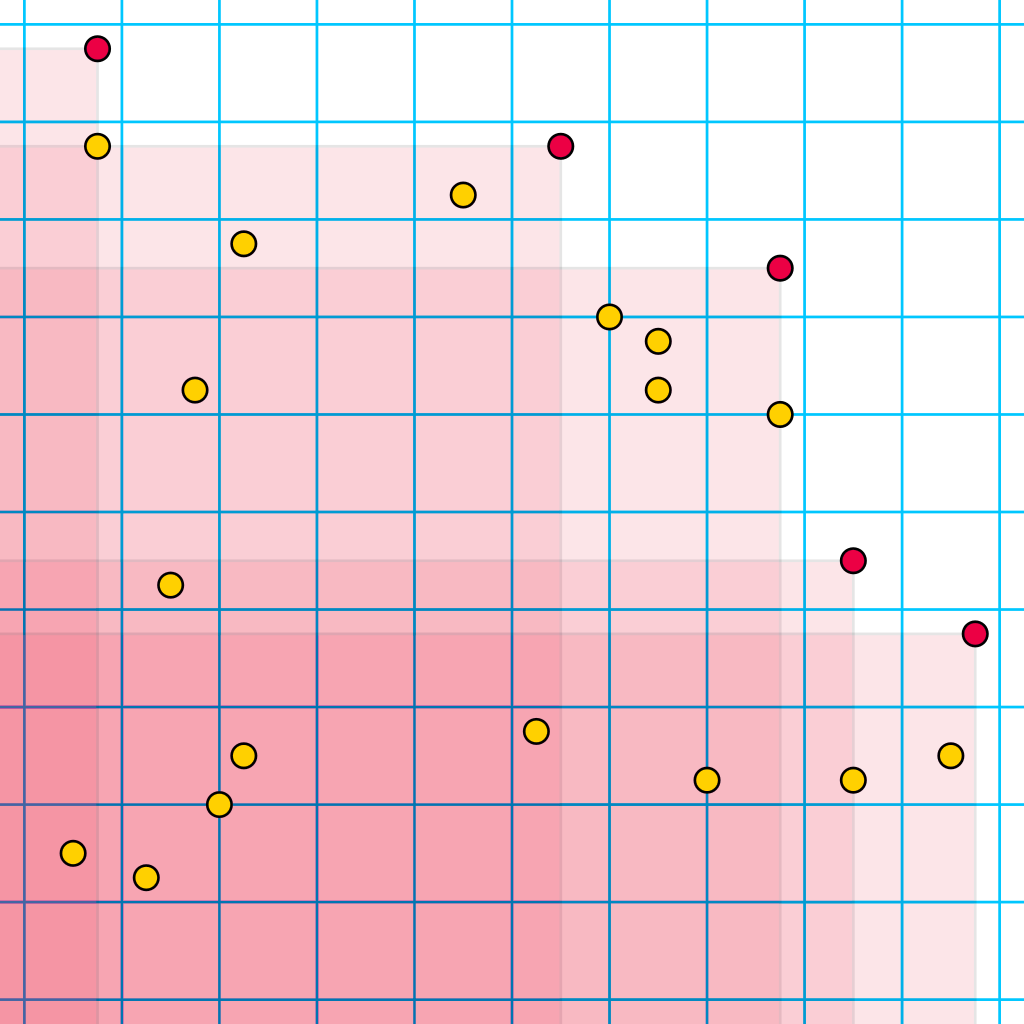
Pareto front



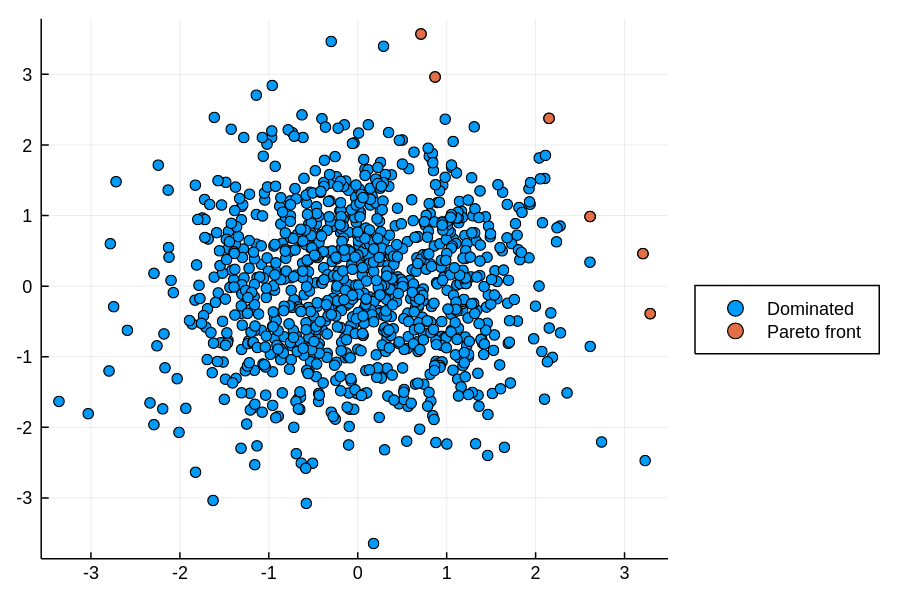
    The Pareto Front is the set of Pareto Optimal solutions.
    Red points are non-dominated by each other and dominate the other points.

Pareto front


NSGA-II Overview



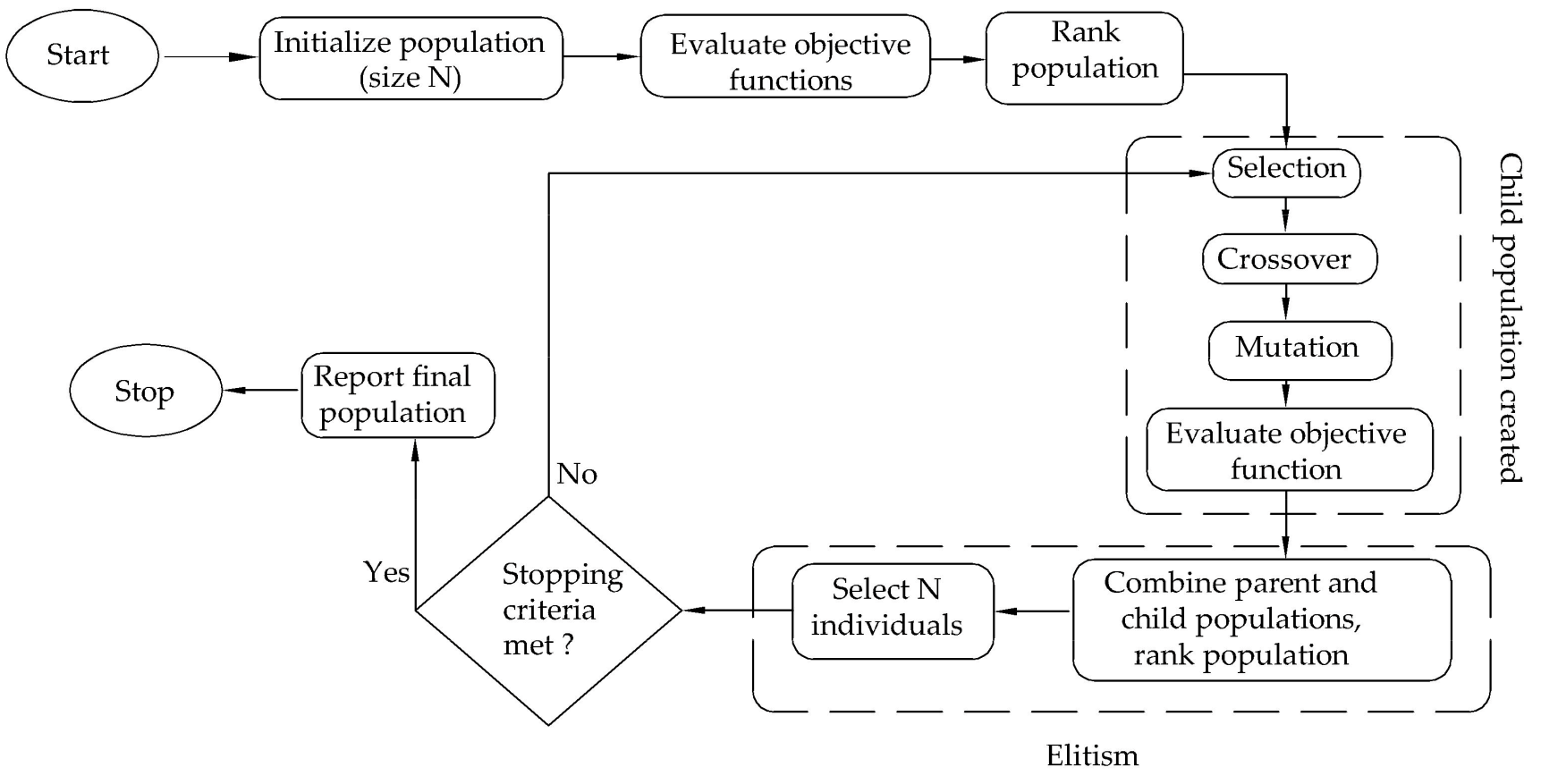
Deb, Kalyanmoy, et al. "A fast and elitist multiobjective genetic algorithm: NSGA-II." IEEE transactions on evolutionary computation 6.2 (2002): 182-197. [pdf]

Non-dominated sorting



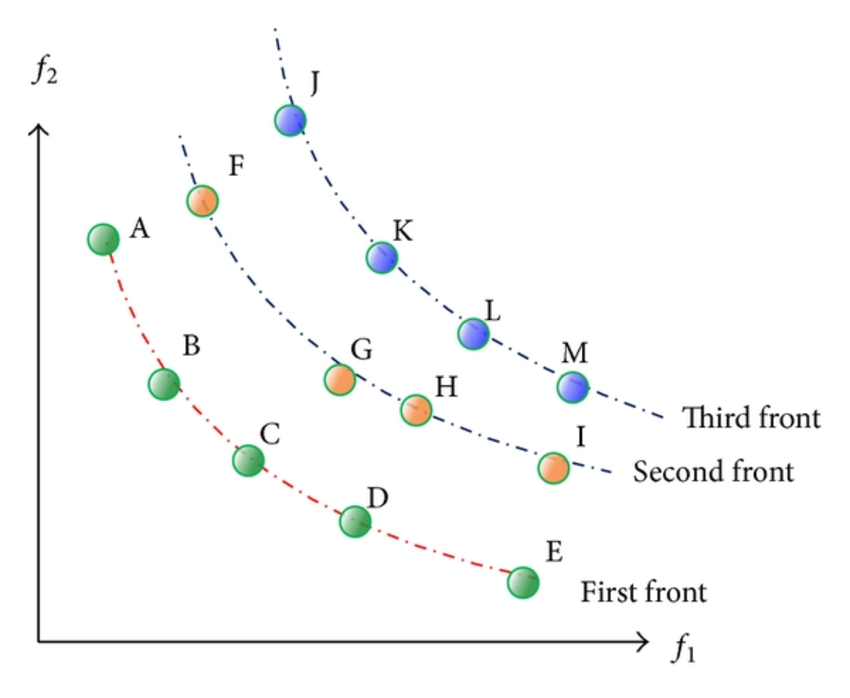
Wang, H. S., C. H. Tu, and K. H. Chen. "Supplier selection and production planning by using guided genetic algorithm and dynamic nondominated sorting genetic algorithm II approaches." Mathematical Problems in Engineering 2015 (2015).

Crowding Distance Assignment



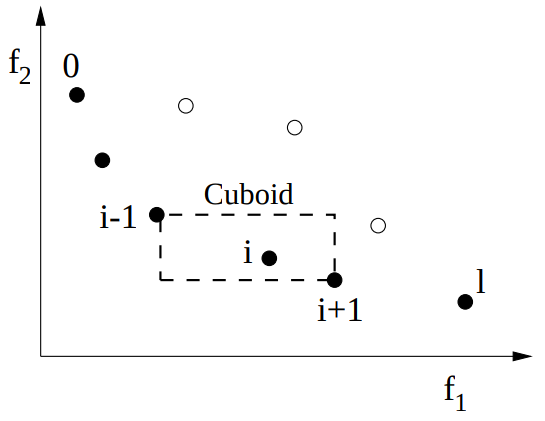
Deb, Kalyanmoy, et al. "A fast and elitist multiobjective genetic algorithm: NSGA-II." IEEE transactions on evolutionary computation 6.2 (2002): 182-197. [pdf]

NSGA-II Overview




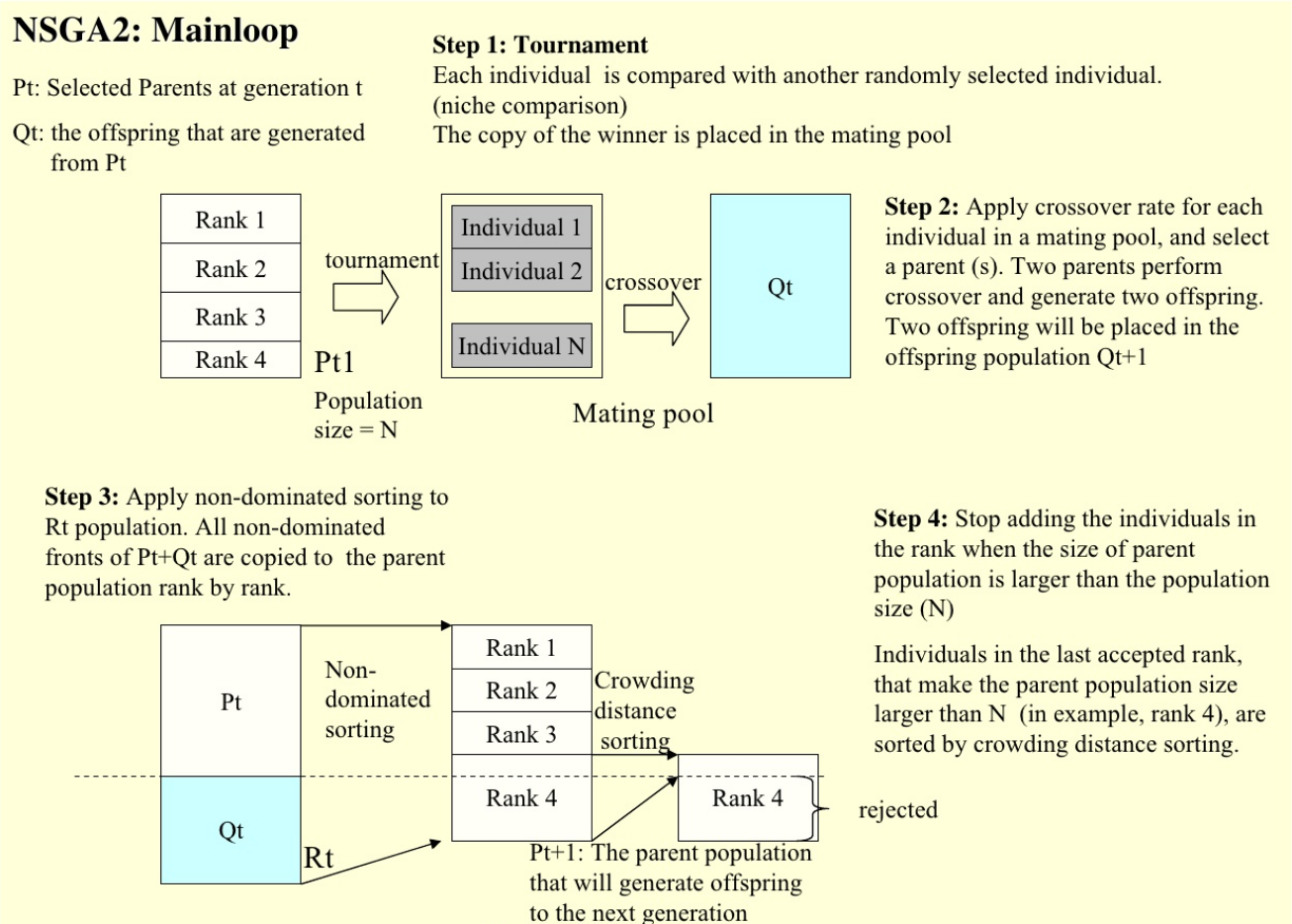
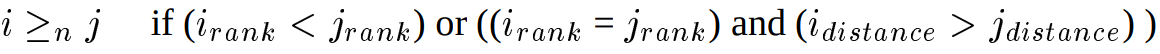
Deb, Kalyanmoy, et al. "A fast and elitist multiobjective genetic algorithm: NSGA-II." IEEE transactions on evolutionary computation 6.2 (2002): 182-197. [pdf]

Problems with Pareto




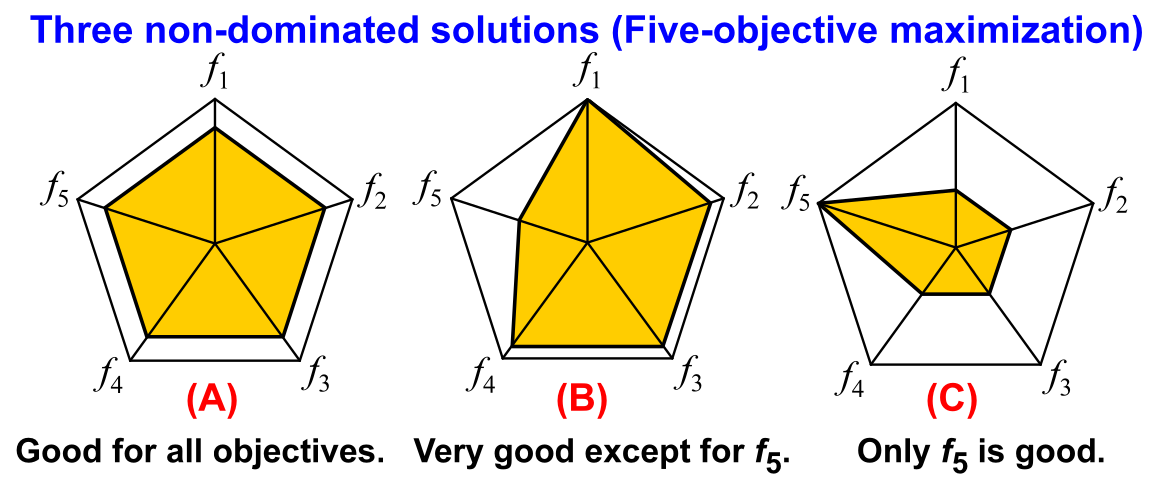
Ishibuchi, Hisao, and Hiroyuki Sato. "Evolutionary many-objective optimization." Proceedings of the Genetic and Evolutionary Computation Conference Companion. 2019.

Many-objective optimization




Ishibuchi, Hisao, and Hiroyuki Sato. "Evolutionary many-objective optimization." Proceedings of the Genetic and Evolutionary Computation Conference Companion. 2019.

Exercise 1


Explore some applications of MOEAs.
Choose an article and discuss in your group what the problem is and what the different objectives are.